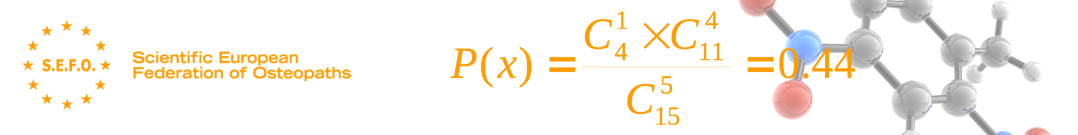[ezcol_1half]
STATISTIQUE DESCRIPTIVE
Elle décrit ou ordonne un ensemble de données qui sont brutes.
[/ezcol_1half]
[ezcol_1half_end]
STATISTIQUE INFERENCIAL
Elle permet que savoir si les relations observées dans une population tendent à se produire dans la population générale.
Elle évalue la variabilité aléatoire et contrôle les facteurs de confusion.
[/ezcol_1half_end]
[ezcol_1half]
MESURES DE TENDANCE CENTRALE
Médiane.
Mode.
Moyenne.
Intervalle de confiance.
[/ezcol_1half]
[ezcol_1half_end]
MESURES DE DISPERSION
Déviation Standard.
Rang.
Variance.
[/ezcol_1half_end]
[ezcol_1half]
CONCEPTION EXPÉRIMENTALE
Elle cherche des différences entre deux ou plus ensembles de données.
[/ezcol_1half]
[ezcol_1half_end]
CONCEPTION DE CORRÉLATION
Elle cherche des similitudes entre deux ou plus ensembles de données.
[/ezcol_1half_end]
CE QUE DOIVENT MESURER LES STATISTIQUES
1º MOYENNE:
Moyenne de la population d’où proviennent les échantillons.
2º DÉVIATION STANDARD:
Il s’agit de la mesure de la dispersion de la variable dans la population et dans l’échantillon, respectivement.
C’est une statistique utilisée comme mesure de dispersion ou de variation dans une distribution, égale à la racine carrée de la moyenne arithmétique des carrés des déviations de la moyenne arithmétique.
- C’est une mesure de la dispersion d’un groupe de données à partir de sa moyenne. Plus il existe de différence entre les données, plus haute est la déviation.
- Elle a les mêmes unités que la variable. La déviation typique est invariable par rapport à l’origine de la distribution.
La déviation standard peut aussi être calculée comme la racine carrée de la variation.
3º INTERVALLE DE CONFIANCE:
C’est un rang de valeurs dans lequel on trouve la véritable valeur d’un paramètre ou une estimation d’un ensemble d’observations.
Il permet de connaître la précision d’une étude.
Différents échantillons conduiraient à différents résultats, on a besoin d’une mesure de la précision de cette estimation, c’est ce que fait le calcul de l’intervalle de confiance (IC= 95%).
On ne peut pas indiquer une variable sans son intervalle de confiance, c’est ce qui lui donne une précision (95% 5 % d’erreur est très bon, on laisse toujours 5% de marge d’erreur).
4º EPREUVE DE REFERENCE OU « GOLD STANDARD »:
Il s’agit de n’importe quelle épreuve admise comme référence standard de traitement ou de diagnostic pour une maladie particulière.
5º SENSIBILITÉ: Taux de véritables positifs.
C’est la probabilité de l’épreuve pour trouver une maladie parmi ceux qui présentent la maladie ou la proportion de gens avec maladie qui donne un résultat positif lors de d’épreuve.
Sensibilité = vrais positifs/ (vrais positifs + faux négatifs)
Elle se réfère à une épreuve diagnostique, c’est la proportion de personnes véritablement malades qui ont été cataloguées comme telles par cette épreuve.
6º SPÉCIFICITÉ:
C’est la probabilité que le test ne trouve aucune maladie parmi ceux qui ne présentent pas la maladie ou la proportion de gens sans maladie qui présentent une épreuve négative.
Spécificité = vrais négatifs (vrais négatifs + faux positifs)
7º DISTRIBUTION NORMALE : n.
C’est une distribution de fréquence théorique pour un système de données variables, représenté généralement par une courbe en cloche de Gauss symétrique.
8º TENDANCE CENTRALE:
C’est le centre d’une distribution. Elle est décrite par la moyenne, le point moyen, et la mode.
- Moyenne : La moyenne arithmétique dans un système de valeurs. C’est une mesure de centralisation pour une variable continue. On l’obtient en sommant toutes les valeurs d’échantillon et en les divisant par la taille de l’échantillon. Seulement pour une variable quantitative. Valeur uniforme que devrait présenter chaque individu d’un ensemble (population ou échantillon) pour que le total de l’ensemble soit inchangé. C’est, dans le cas de la moyenne arithmétique, le quotient de la somme par l’effectif. Contre exemple de condensateurs en série : La capacité moyenne est la moyenne harmonique des capacités. La moyenne est une statistique dite de tendance centrale.
- Médiane : Pour un système de valeurs disposées en ordre de grandeur, la médiane est la valeur moyenne pour les nombres impaire de valeurs et la moyenne des deux valeurs moyennes pour un nombre paire de valeurs. Dans une population ou dans un échantillon, c’est la valeur qu’occupe la position centrale quand toutes les valeurs sont disposées du plus grand vers le plus petit. Dans une distribution normale la moyenne correspond au percentile 50%. C’est-à-dire, que la moyenne fait qu’il y ait 50% de valeurs d’échantillonnage inférieures à elle et 50% de valeurs d’échantillonnage supérieures à elle.
- Mode : Pour un système de valeurs, dans une population c’est la valeur plus fréquente d’une série d’observations. C’est la valeur qui se répète dans une variable nominale.
9º INCIDENCE:
L’incidence représente le nombre de nouveaux « cas » dans une période de temps.
C’est un indexe dynamique qui requiert un suivi de la population d’intérêt dans le temps.
Elle peut être mesuré avec deux indexes : l’incidence accumulée et la densité (ou le taux d’incidence).
L’incidence accumulée est la proportion d’individus qui développent l’événement pendant la période de suivi.
Taux d’incidence.
C’est le nombre de nouveaux cas d’une maladie ou d’autres événements pendant une période déterminée, divisée par le nombre de personnes exposées au risque pendant cette période.
10º PRÉVALENCE:
C’est la proportion d’individus d’une population qui présentent l’événement durant un moment, ou une période de temps, déterminé. C’est le nombre de cas d’une maladie dans une population et à un moment donné.
Par exemple la prévalence de diabète à Madrid durant l’année 2001 est la proportion d’individus de cette province qui durant l’année 2001 souffraient la maladie.
Taux de prévalence.
C’est le nombre total d’individus qui présentent un attribut ou souffrent d’une maladie dans un moment ou une période déterminée, divisé par la population courant le risque d’avoir l’attribut ou la maladie à ce moment ou à la moitié de la période considérée.
11º VARIANCE:
Elle mesure la dispersion de la variable autour de la moyenne.
C’est la valeur attendue ou l’espoir mathématique.
C’est une mesure de la variation d’une série d’observations ; elle est égale à la somme des carrés des déviations par rapport à la médiane, divisée par le nombre de degrés de liberté de la série. Sa racine carrée est la déviation standard.
12º AMPLITUDE OU RANG:
C’est la différence entre la valeur maximale (qui est une valeur d’échantillonnage au-dessus de laquelle il n’ya pas de valeurs d’échantillonnage) et minimale (qui est une valeur d’échantillonnage au dessous de laquelle il n’y a pas de valeurs d’échantillonnage) des valeurs d’une variable.
Dans l’amplitude d’une variable sont compris 100% des valeurs de l’échantillon.
C’est la différence entre la valeur maximale et minimale d’un échantillon ou d’une population. Elle est seulement valable dans des variables continues.
13º MESURE DE LA DISPERSION D’UN ECHANTILLON:
C’est la racine carrée positive de la variance.
![]()
Si l’échantillon consiste en n valeurs d’une variable et, c’est-à-dire, la déviation standard de y dans l’échantillon sera:
Où y est la moyenne de l’échantillonnage. Entre -1 et +1 de déviations standards sont inclue 68.3% des observations ; entre -2 et +2, 95.4% et entre -3 et +3 pratiquement 99.7% ; par conséquent, dans une distribution normale on espère que seulement 0.3% des observations effectuées diffèrent de la moyenne dans plus de trois déviations standards.
14º DIFFÉRENCES STATISTIQUEMENT SIGNIFICATIVES:
Il s’agit des différences entre ce qui est observé et ce qui est supposé l’être dans l’hypothèse nulle qui ne peuvent pas être expliquées par le hasard.
15º DISTRIBUTION BIMODALE:
C’est la distribution de fréquences avec deux zones de densité de fréquence (lesquelles déterminent deux modes) séparées par une zone intermédiaire de basse fréquence d’observations.
16º DISTRIBUTION BINÔMIALE:
C’est la distribution de la probabilité d’observer x événements au cours de n observations indépendantes dans lesquelles on suppose qu’il existe, dans chaque observation, une probabilité p identique d’apparition de l’événement.
Le résultat de chaque épreuve doit être dichotomique, c’est-à-dire, avec deux possibilités qui s’excluent mutuellement (par exemple, la présence ou l’absence de maladie).
17º CONCEPTION FACTORIELLE:
Conception appliquée dans des études dans lesquels deux traitements ou sont testés prouvés séparément ou ensembles, de sorte qu’on puisse mesurer les interactions entre eux.
Si l’étude inclut deux drogues ou interventions thérapeutiques A et B, on forme quatre groupes : traité avec A et placebo de B, un autre traité avec B et placebo de A, un autre traité simultanément avec A et B, et un autre traité avec le placebo de A + le placebo de B.
18º DISTRIBUTION DE FRÉQUENCES:
Graphique ou tableau dans lequel se montre la fréquence dans laquelle une valeur ou une caractéristique se présente dans une population ou un échantillon par catégories ou sous-groupes.
Sa position générale dans une échelle est décrite avec une mesure de tendance centrale ; il y a trois mesures de tendance centrale : la moyenne, la médiane et la mode.
La déviation standard informe sur la dispersion de la valeur mesurée dans la population étudiée.
19º DISTRIBUTION DE POISSON:
C’est la distribution de la probabilité d’observer x épisodes d’un événement quand on attend n dans une période donnée.
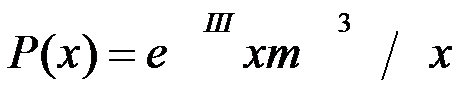
La distribution de Poisson dérive de la distribution binomiale quand le nombre n d’observations tendra vers l’infini (dans la pratique, quand il sera supérieur à 100) et la probabilité (qui est supposée constante dans chaque observation) que l’apparition de l’événement P tende à zéro.
La distribution de Poisson est utilisée souvent en pharmacovigilance et en pharmaco-épidémiologie quand on étudie des risques bas dans des populations de plus de 100 effectifs, afin de calculer la probabilité d’apparition d’un certain événement, de calculer l’intervalle de confiance d’un taux, d’estimer le nombre d’individus qui doivent être inclus dans une étude, etc.
20º DISTRIBUTION NORMALE OU DE GAUSS:
C’est une distribution théorique de probabilité qui est utilisée tant dans la statistique appliquée comme dans la théorique.
Elle apparaît dans la pratique très fréquemment comme conséquence de l’important résultat qui établit le théorème central de la limite.
Elle a une forme de cloche, et est caractérisée par uniquement deux valeurs : la moyenne et la variance.
C’est une distribution de fréquences continue, symétrique, avec deux queues qui s’étendent vers l’infini, dans laquelle la moyenne, la médiane et la mode ont la même valeur et dont la forme est déterminée par la moyenne et la déviation standard.
21º META-ANÁLISIS:
Il s’agit de l’intégration structurée et systématique de l’information obtenue dans différentes études sur un problème déterminé.
Elle consiste à identifier et à réviser les études contrôlées sur un certain problème, afin de donner une estimation quantitative synthétique de toutes les études disponibles.
Puisqu’elle inclut un nombre plus grand d’observations, une méta-analyse a un pouvoir statistique supérieur des aux études cliniques qu’elle inclut.
Les deux principaux problèmes méthodologiques de la méta-analyse des études cliniques sont:
1) L’hétérogénéité dans les études inclues (en termes de caractéristiques cliniques et sociodémographiques des populations inclues dans chaque étude, des méthodes d’évaluation clinique appliquées, la dose, la forme pharmaceutique ou la règle de dosage du médicament évalué, etc.).
2) Les possibles erreurs de publication (dérivés du fait que toutes les études cliniques réellement effectués n’ont pas toutes été publiées).
22º MODÈLE LINÉAIRE:
C’est modèle statistique dans lequel la valeur d’un paramètre y est égale à a + bx, où a (ordonnée à l’origine) et b (en suspens, dont la valeur est inclue entre -1 et +1) sont constants.
23º MODÈLE LOGISTIQUE :
![]() C’est un modèle statistique de probabilité de la maladie et e fonction d’un facteur de risque x, dans lequel où P (y/x) est la probabilité qu’apparaisse y parmi les exposés au facteur x et y, c’est la fonction exponentielle naturelle.
C’est un modèle statistique de probabilité de la maladie et e fonction d’un facteur de risque x, dans lequel où P (y/x) est la probabilité qu’apparaisse y parmi les exposés au facteur x et y, c’est la fonction exponentielle naturelle.
![]() Dans le modèle logistique multiple le terme fix est remplacé par un terme linéaire qui comprend plusieurs facteurs, par exemple : s’il existe deux facteurs x1 et x2
Dans le modèle logistique multiple le terme fix est remplacé par un terme linéaire qui comprend plusieurs facteurs, par exemple : s’il existe deux facteurs x1 et x2
24º NIVEAU DE SIGNIFICATION:
Dans les tests de signification statistique, c’est la valeur de p, laquelle dans un sens strict, dans une étude clinique celle-ci doit être pré-spécifié dans la phase de conception.
Le niveau admis avec la plus grande fréquence est de 0.05, mais on peut aussi appliquer des niveaux de 0.01, 0.001, etc.
25º NOMBRE QU’IL EST NÉCESSAIRE DE TRAITER (NNT):
Quand le traitement expérimental augmentera la probabilité d’un événement favorable (ou quand il diminuera celle d’un événement défavorable), c’est le nombre de patients qu’il faut traiter pour donner lieu à un patient avec plus d’amélioration (ou pour prévenir un événement adverse additionnel).
Il est calculé comme 1/RAR, arrondi au numéro entier immédiatement suivant, accompagné d’un intervalle de confiance de 95%.
26º P (p-valeur):
C’est le niveau de signification observé dans le test.
Plus P est petit, plus grandes seront les preuves pour rejeter l’hypothèse nulle.
27º P (PROBABILITÉ).
Suivie de l’abréviation n.s. (non significative) ou du symbole < (inférieur à) et d’un chiffre décimal (par exemple 0.05 ou 0.01), il indique la probabilité que la différence observée dans un échantillon ne soit purement produite par hasard, les groupes comparés étant réellement semblables, c’est-à-dire en dessous de l’hypothèse nulle.
28º PERCENTIL:
Percentile 90% correspond à une valeur qui divise à l’échantillon en deux, de sorte qu’il y ait 90% de valeurs d’échantillonnage inférieures à celui-ci, et 10% de valeurs d’échantillonnage supérieures à celui-ci.
Les percentiles 25%, 50%, 75% sont le premier, le second et troisième quartile respectivement.
Dans une série (suffisamment grande) d’observations ordonnées (par exemple, du plus petit au plus grand), la partie qui constitue un pourcentage déterminé de tous les éléments de la série.
Par exemple, dans une série de valeurs de hauteur (en cm), le premier percentile 10 sera constitués par les poids de 10% des individus les plus petits, et le dixième percentile 10 sera constitués par 10% de sujets les plus grands.
De la même manière, le premier quartile ou le premier quintile consisteraient, respectivement, 25% et 20% des individus plus petits.
Dans une distribution normale, la médiane équivaut précisément au percentile 50 (50% des individus sont au dessus et 50% sont en dessous de la médiane).
29 º COEFFICIENT DE CORRÉLATION:
C’est une mesure d’association qui indique le degré dans lequel deux variables continues x et y possèdent une relation linéaire (y = a ± bx).
Il est désigné par la lettre r, et sa valeur peut se situer entre -1 et +1.
Les valeurs -1 et +1 – indiquent qu’il existe une relation linéaire parfaite, négative ou positive respectivement, entre les deux variables, et dans une représentation dans des axes de coordonnées, les données sont distribuées sous forme de droite, avec une pente négative ou positive, respectivement.
Quand r = 0, les données seront disposées sous forme de cercle et il n’existe aucun degré de corrélation.
30º COEFFICIENT DE VARIATION:
C’est la déviation standard exprimée comme pourcentage de la moyenne, c’est-à-dire (DE/x) X 100.
31º SIGNIFICATION CLINIQUE:
C’est la probabilité qu’une différence observée ait une répercussion sur le cours du problème ou de la maladie traités soit significative pour un patient donné ou pour un ensemble de patients.
Elle ne doit pas être confondue avec la signification statistique : les descriptions de différences statistiquement significatives qui ne sont pas cliniquement significatives sont fréquentes.
32º SIGNIFICATION STATISTIQUE:
C’est la probabilité qu’une différence observée soit le résultat du hasard et non des causes déterminantes causales dans une étude.
La découverte d’une signification statistique n’implique pas nécessairement une signification clinique.
33º TABLE DE CONTINGENCE:
Tableaux de 2 ou plus variables, où dans chaque case on comptabilise les individus qui appartiennent à chaque combinaison des possibles niveaux de ces variables.
Gazéification tabulaire de données d’un échantillon de population, dans laquelle les sous-catégories d’une caractéristique s’indiquent horizontalement (dans des files) et celles des autres verticalement (dans des colonnes).
On peut ainsi appliquer des tests d’association entre les caractéristiques des files et celles des colonnes.
Le tableau de contingence le plus simple est celui de 2 X 2, dans laquelle on inclut deux catégories de la caractéristique des files et deux catégories de la caractéristique des colonnes (c’est-à-dire de quatre valeurs).
Pour examiner les résultats d’une étude clinique, se disposent généralement dans la file supérieure les données relatives au groupe expérimental, et dans l’inférieur celles correspondant au groupe contrôle.
Dans la première colonne on dispose généralement le nombre de patients qui présentent l’événement étudié, et dans le second le nombre de ceux qui n’ont pas présenté l’événement.