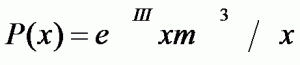[ezcol_1half]
ESTADÍSTICA DESCRIPTIVA
- Describe u ordena un conjunto de datos que están en bruto.
[/ezcol_1half]
[ezcol_1half_end]
ESTADÍSTICA INFERENCIAL
- Permite saber sí las relaciones observadas en una muestra tienden a ocurrir en la población general.
- Evalúa la variabilidad aleatoria y controla los factores de confusión.
[/ezcol_1half_end]
[ezcol_1half]
MEDIDAS DE TENDENCIA CENTRAL
- Media.
- Moda.
- Mediana.
- Intervalo de confianza.
[/ezcol_1half]
[ezcol_1half_end]
MEDIDAS DE DISPERSIÓN
- Desviación Estándar.
- Rango.
- Varianza.
[/ezcol_1half_end]
[ezcol_1half]
DISEÑO EXPERIMENTAL
- Busca diferencias entre dos o más conjuntos de datos.
[/ezcol_1half]
[ezcol_1half_end]
DISEÑO DE CORRELACIÓN
- Busca similitudes entre dos o más conjuntos de datos.
[/ezcol_1half_end]
LO QUE DEBEN MEDIR LAS ESTADÍSTICAS
1º MEDIA:
Media de la población de la que proceden las muestras.
2º DESVIACIÓN ESTÁNDAR: σ o s
Son medidas de la dispersión de los valores de la variable en la población y en la muestra, respectivamente.
Es una estadística usada como medida de dispersión o de variación en una distribución, igual a la raíz cuadrada de la media aritmética de los cuadrados de las desviaciones de la media aritmética.
- Medida de la dispersión de un grupo de datos a partir de su media. Más diferencia entre los datos hay, más alta es la desviación.
- Tiene las mismas unidades que la variable. La desviación típica es invariante con respecto al origen de la distribución.
La desviación de estándar se puede también calcular como la raíz cuadrada de la variación.
3º INTERVALO DE CONFIANZA:
Es un rango de valores entre el que se encuentra el verdadero valor de un parámetro o estimación de un conjunto de observaciones.
Permite conocer la precisión del estudio.
Diferentes muestras conducirían a diferentes resultados, se necesita una medida de la precisión de esta estimación, lo que hace el cálculo del intervalo de confianza (IC= 95%).
No se puede indicar una variable sin su intervalo de confianza, es lo que da precisión (95% es muy bueno, siempre se deja 5 % de error).
4º ESTÁNDAR DE ORO o “GOLD STANDARD”:
Prueba aceptada de referencia estándar o de diagnóstico para una enfermedad particular.
5º SENSIBILIDAD: Tasa de verdaderos positivos.
La probabilidad de la prueba para encontrar una enfermedad entre los que tienen la enfermedad o la proporción de la gente con enfermedad que tiene un resultado de prueba positiva.
Sensibilidad = verdaderos positivos / (verdaderos positivos + falsos negativos)
Referida a una prueba diagnóstica, es la proporción de personas verdaderamente enfermas que han sido catalogadas como tales mediante dicha prueba.
6º ESPECIFICIDAD:
Es la probabilidad que el test no encuentra NINGUNA enfermedad entre los que no tienen la enfermedad o la proporción de la gente sin enfermedad que tiene una prueba negativa.
Especificidad = negativas verdaderas/ (negativas verdaderas + positivos falsos)
7º DISTRIBUCIÓN NORMAL: n.
Una distribución de frecuencia teórica para un sistema de datos variables, representado generalmente por una curva acampanada de Gauss simétrica sobre el medio.
8º TENDENCIA CENTRAL:
El centro de una distribución. Descrito por media, punto medio, y moda.
- Media: La media aritmética en un sistema de valores. El promedio. Es una medida de centralización para una variable continua. Se obtiene sumado todos los valores muéstrales y dividiendo por el tamaño muestral.
- Mediana: Para un sistema de valores dispuestos en orden de magnitud, la mediana es el valor medio para los números impares de valores y el promedio de los dos valores medios para un número par de valores. En una población o en una muestra, es el valor que ocupa la posición central cuando todos los valores se disponen en orden de mayor a menor. En una distribución normal la mediana corresponde al percentil 50%. Es decir, la mediana hace que haya un 50% de valores muéstrales inferiores a ella y un 50% de valores muéstrales superiores a ella.
- Moda: Para un sistema de valores, en una población es el valor más frecuente de una serie de observaciones. Es el valor que más se repite en una variable nominal.
9º INCIDENCIA:
La incidencia refleja el número de nuevos “casos” en un periodo de tiempo.
Es un índice dinámico que requiere seguimiento en el tiempo de la población de interés.
Se puede medir con dos índices: incidencia acumulada y densidad (o tasa) de incidencia.
La incidencia acumulada es la proporción de individuos que desarrollan el evento durante el periodo de seguimiento.
Tasa de incidencia.
Número de nuevos casos de una enfermedad u otros acontecimientos durante un período determinado, dividido por el número de personas expuestas al riesgo durante este período.
10º PREVALENCIA:
Es la proporción de individuos de una población que presentan el evento en un momento, o periodo de tiempo, determinado. Número de casos de una enfermedad en una población y en un momento dados.
Por ejemplo la prevalencia de diabetes en Madrid en el año 2001 es la proporción de individuos de esa provincia que en el año 2001 padecían la enfermedad.
Tasa de prevalencia.
Número total de individuos que presentan un atributo o padecen una enfermedad en un momento o período determinado, dividido por la población en riesgo de tener el atributo o la enfermedad en dicho momento o en mitad del período considerado.
11º VARIANZA:
Mide la dispersión de la variable alrededor de la media.
Valor esperado o esperanza matemática o media.
Medida de la variación de una serie de observaciones; es igual a la suma de los cuadrados de las desviaciones respecto a la media, dividida por el número de grados de libertad de la serie. Su raíz cuadrada es la desviación estándar.
12º AMPLITUD O RANGO:
La diferencia entre el valor máximo (Es un valor muestral de forma que por encima de este no hay valores muéstrales) y mínimo (Es un valor muestral de forma que por debajo de este no hay valores muéstrales) de los valores de una variable.
En la amplitud de una variable se encuentran comprendidos el 100% de los valores muéstrales.
Diferencia entre el valor máximo y mínimo de una muestra o población. Solo es válido en variables continuas.
13º MEDIDA DE LA DISPERSIÓN DE UNA MUESTRA:
Es la raíz cuadrada positiva de la varianza.
Si la muestra consiste en n valores de una variable y, es decir ,![]() la desviación estándar de y en la muestra será:
la desviación estándar de y en la muestra será: ![]()
Donde y es la media de la muestra. Entre -1 y +1 desviaciones estándar se incluye un 68,3% de las observaciones; entre -2 y +2, un 95,4% y entre -3 y +3 prácticamente un 99,7%; por lo tanto, en una distribución normal se espera que sólo un 0,3% de las observaciones realizadas difieran de la media en más de tres desviaciones estándar.
14º DIFERENCIAS ESTADÍSTICAMENTE SIGNIFICATIVAS:
Las diferencias entre lo observado y lo supuesto en la hipótesis nula no pueden ser explicadas por el azar.
15º DISTRIBUCIÓN BIMODAL:
Distribución de frecuencias con dos zonas de densidad de frecuencia (las cuales determinan dos modas) separadas por una zona intermedia de baja frecuencia de observaciones.
16º DISTRIBUCIÓN BINOMIAL:
Distribución de la probabilidad de observar x acontecimientos en el curso de n observaciones independientes en la que se supone, en cada observación, una probabilidad p idéntica de aparición del acontecimiento.
El resultado de cada prueba debe ser dicotómico, es decir, con dos posibilidades que se excluyen mutuamente (por ejemplo, presencia o ausencia de enfermedad).
17º DISEÑO FACTORIAL:
Diseño aplicado en ensayos en los que dos o más tratamientos son probados por separado o al unísono, de modo que se pueden medir interacciones entre ellos.
Si el ensayo incluye dos fármacos o intervenciones terapéuticas A y B, se forman cuatro grupos: uno tratado con A y placebo de B, otro tratado con B y placebo de A, otro tratado simultáneamente con A y B, y otro tratado con placebo de A + placebo de B.
18º DISTRIBUCIÓN DE FRECUENCIAS:
Gráfica o tabla en la que se muestra la frecuencia con la que un valor o característica se presenta en una población o muestra por categorías o subgrupos.
Su posición general en una escala se describe con una medida de tendencia central; hay tres medidas de tendencia central: la media, la mediana y la moda.
La desviación estándar informa sobre la dispersión del valor medido en la población estudiada.
19º DISTRIBUCIÓN DE POISSON:
Distribución de la probabilidad de observar x episodios de un acontecimiento cuando se esperan m en un período dado.
La distribución de Poisson deriva de la distribución binomial cuando el número n de observaciones tiende a infinito (en la práctica, cuando es superior a 100) y la probabilidad (que se supone constante en cada observación) de aparición del acontecimiento P tiende a cero.
La distribución de Poisson se utiliza a menudo en fármaco vigilancia y fármaco epidemiología cuando se estudian riesgos bajos en poblaciones de más de 100 efectivos, con el fin de calcular la probabilidad de aparición de un determinado acontecimiento, calcular el intervalo de confianza de una tasa, estimar el número de individuos que deben ser incluidos en un estudio, etc.
20º DISTRIBUCIÓN NORMAL O DE GAUSS:
Es una distribución teórica de probabilidad que se usa tanto en la estadística aplicada como en la teórica.
Aparece en la práctica con mucha frecuencia como consecuencia del importante resultado que establece el teorema central del límite.
Tiene una forma en forma de campana, y viene caracterizada por únicamente dos valores: la media y la varianza.
Distribución de frecuencias continua, simétrica, con dos colas que se extienden hacia el infinito, en la que la media, la mediana y la moda tienen el mismo valor y cuya forma viene determinada por la media y la desviación estándar.
21º META-ANÁLISIS:
Integración estructurada y sistemática de la información obtenida en diferentes estudios sobre un problema determinado.
Consiste en identificar y revisar los estudios controlados sobre un determinado problema, con el fin de dar una estimación cuantitativa sintética de todos los estudios disponibles.
Dado que incluye un número mayor de observaciones, una meta-análisis tiene un poder estadístico superior al de los ensayos clínicos que incluye.
Los dos principales problemas metodológicos de la meta-análisis de ensayos clínicos son:
la heterogeneidad entre los ensayos incluidos (en términos de características clínicas y socio-demográficas de las poblaciones incluidas en cada ensayo, los métodos de evaluación clínica aplicados, la dosis, forma farmacéutica o pauta de dosificación del fármaco evaluado, etc.).
el posible sesgo de publicación (derivado de que no todos los ensayos clínicos realmente realizados han sido publicados).
22º MODELO LINEAL:
Modelo estadístico en el que el valor de un parámetro y es igual a a + bx, en donde a (ordenada en el origen) y b (pendiente, cuyo valor está incluido entre -1 y +1) son constantes.
23º MODELO LOGÍSTICO:
Modelo estadístico de probabilidad de la enfermedad y en función de un factor de riesgo x, en el que![]() en donde P (y/x) es la probabilidad de que aparezca y entre los expuestos al factor x y e es la función exponencial natural.
en donde P (y/x) es la probabilidad de que aparezca y entre los expuestos al factor x y e es la función exponencial natural.
En el modelo logístico múltiple el término fix es sustituido por un término lineal que comprende varios factores, por ejemplo:![]() si existen dos factores x1 y x2
si existen dos factores x1 y x2
24º NIVEL DE SIGNIFICACIÓN:
En las pruebas de significación estadística, es el valor de p, el cual, en sentido estricto, en un ensayo clínico debe ser pre especificado en la fase de diseño.
El nivel aceptado con mayor frecuencia es de 0,05, pero también se pueden aplicar niveles de 0,01, 0,001, etc.
25º NÚMERO QUE ES NECESARIO TRATAR (NNT):
Cuando el tratamiento experimental incrementa la probabilidad de un acontecimiento favorable (o cuando disminuye la de un acontecimiento adverso), número de pacientes que hay que tratar para dar lugar a un paciente más con mejoría (o para prevenir un acontecimiento adverso adicional).
Se calcula como 1/RAR, redondeado al número entero inmediatamente siguiente, acompañado de un intervalo de confianza al 95%.
26º P (p- valor):
El nivel de significación observado en el test.
Cuanto más pequeño sea, mayor será la evidencia para rechazar la hipótesis nula.
27º P (PROBABILIDAD).
Seguida de la abreviatura n.s. (no significativa) o del símbolo < (inferior a) y una cifra decimal (por ejemplo 0,05 o 0,01), indica la probabilidad de que la diferencia observada en una muestra haya ocurrido puramente por azar siendo los grupos comparados realmente semejantes, es decir bajo la hipótesis nula.
28º PERCENTIL:
Un percentil 90% corresponde a un valor que divide a la muestra en dos, de forma que hay un 90% de valores muéstrales inferiores a éste, y un 10% de valores muéstrales superiores a éste.
Los percentiles 25%, 50%, 75% son el primer, segundo y tercer cuartil respectivamente.
En una serie (suficientemente grande) de observaciones ordenadas (por ejemplo, de menor a mayor), la parte que constituye un porcentaje determinado de todos los elementos de la serie.
Por ejemplo, en una serie de valores de altura (en cm), el primer percentil 10 estará constituido por los pesos del 10% de individuos más bajos, y el décimo percentil 10 estará constituido por el 10% de sujetos más altos.
Análogamente, el primer cuartil o el primer quintil consistirían, respectivamente, en el 25% y el 20% de individuos más bajos.
En una distribución normal, la mediana equivale exactamente al percentil 50 (un 50% de los individuos están por encima y un 50% por debajo de la mediana).
29º COEFICIENTE DE CORRELACIÓN:
Medida de asociación que indica el grado en el que dos variables continuas x e y poseen una relación lineal (y = a ± bx).
Se designa con la letra r, y su valor puede situarse entre -1 y +1.
Los valores -1 y +1 – indican que existe una relación lineal perfecta, negativa o positiva respectivamente, entre ambas variables, y en una representación en ejes de coordenadas los datos se distribuyen en forma de recta, con pendiente negativa o positiva, respectivamente.
Cuando r = 0, los datos se disponen en forma de círculo y no existe ningún grado de correlación.
30º COEFICIENTE DE VARIACIÓN:
Desviación estándar expresada como porcentaje de la media, es decir (DE/x) X 100.
31º SIGNIFICACIÓN CLÍNICA:
Probabilidad de que una diferencia observada tenga una repercusión sobre el curso del problema o enfermedad tratados que sea relevante para un paciente dado o para un conjunto de pacientes.
No debe confundirse con la significación estadística: son frecuentes las descripciones de diferencias estadísticamente significativas que no son clínicamente significativas.
32º SIGNIFICACIÓN ESTADÍSTICA:
Probabilidad de que una diferencia observada sea resultado de la casualidad y no de los determinantes causales en un estudio.
El hallazgo de una significación estadística no implica necesariamente significación clínica.
33º TABLA DE CONTINGENCIA:
Tablas de 2 o más variables, donde en cada celda se contabilizan los individuos que pertenecen a cada combinación de los posibles niveles de estas variables.
Gasificación tabular de datos de una muestra de población, en la que las sub-categorías de una característica se indican horizontalmente (en filas) y las de otra verticalmente (en columnas).
Así se pueden aplicar pruebas de asociación entre las características de las filas y las de las columnas.
La tabla de contingencia más simple es la de 2 x 2, en la que se incluyen dos categorías de la característica de las filas y dos categorías de la característica de las columnas (es decir cuatro valores).
Para examinar los resultados de un ensayo clínico, se suelen disponer en la fila superior los datos referentes al grupo experimental, y en la inferior los correspondientes al grupo de referencia.
En la primera columna se suele disponer el número de pacientes que presentan el acontecimiento estudiado, y en la segunda el número de los que no presentaron el acontecimiento.